📍1. BFS와 DFS 8-퍼즐 프로그램
✔️ 게임 보드 표현
class State:
def __init__(self, board, goal, depth=0):
self.board = board
self.depth = depth
self.goal = goal
# i1과 i2를 교환하여서 새로운 상태를 반환한다.
def get_new_board(self, i1, i2, depth):
new_board = self.board[:]
new_board[i1], new_board[i2] = new_board[i2], new_board[i1]
return State(new_board, self.goal, depth)
# 자식 노드를 확장하여서 리스트에 저장하여서 반환한다. #expand 함수를 State 클래스 안으로 이동
def expand(self, depth):
result = []
i = self.board.index(0) # 숫자 0(빈칸)의 위치를 찾는다.
if not i in [0, 3, 6] : # LEFT 연산자
result.append(self.get_new_board(i, i-1, depth))
if not i in [0, 1, 2] : # UP 연산자
result.append(self.get_new_board(i, i-3, depth))
if not i in [2, 5, 8]: # RIGHT 연산자
result.append(self.get_new_board(i, i+1, depth))
if not i in [6, 7, 8]: # DOWN 연산자
result.append(self.get_new_board(i, i+3, depth))
return result
# 객체를 출력할 때 사용한다.
def __str__(self):
return str(self.board[:3]) +"\n"+\
str(self.board[3:6]) +"\n"+\
str(self.board[6:]) +"\n"+\
"------------------"
def __eq__(self, other): # 이것을 정의해야 in 연산자가 올바르게 계산한다.
return self.board == other.board
def __ne__(self, other): # 이것을 정의해야 in 연산자가 올바르게 계산한다.
return self.board != other.board
✔️ 상태 표현
# 초기 상태
puzzle = [2, 8, 3,
1, 6, 4,
7, 0, 5]
# 목표 상태
goal = [1, 2, 3,
8, 0, 4,
7, 6, 5]
✔️ OPEN과 CLOSED 리스트
중복 상태를 막기 위함!
# open 리스트
open_queue = [ ]
open_queue.append(State(puzzle, goal))
closed_queue = [ ]
depth = 0
count=1
while len(open_queue) != 0:
current = open_queue.pop(0) # OPEN 리스트의 앞에서 삭제
print(count)
count += 1
print(current)
if current.board == goal:
print("탐색 성공")
break
depth = current.depth+1
closed_queue.append(current)
if depth > 5 :
continue
for state in current.expand(depth):
if (state in closed_queue) or (state in open_queue): # 이미 거쳐간 노드이면
continue # 노드를 버린다.
else:
open_queue.append(state) # OPEN 리스트의 끝에 추가
✔️ 출력 결과
1
[2, 8, 3]
[1, 6, 4]
[7, 0, 5]
------------------
2
[2, 8, 3]
[1, 6, 4]
[0, 7, 5]
------------------
...
------------------
46
[1, 2, 3]
[8, 0, 4]
[7, 6, 5]
------------------
탐색 성공
📍2. DFS 프로그램
✔️ DFS 탐색은 무한히 깊이 빠져서 돌아 오지 못할 수도 있음
➡️ 깊이 제한 필요. (아래는 변경된 소스 코드)
# 자식 노드를 확장하여서 리스트에 저장하여서 반환한다.
def expand(self, depth):
result = []
if depth > 5: return result # 깊이가 5 이상이면 더 이상 확장을 하지 않는다.
i = self.board.index(0) # 숫자 0(빈칸)의 위치를 찾는다.
if not i in [6, 7, 8]: # DOWN 연산자
result.append(self.get_new_board(i, i+3, moves))
if not i in [2, 5, 8]: # RIGHT 연산자
result.append(self.get_new_board(i, i+1, moves))
if not i in [0, 1, 2] : # UP 연산자
result.append(self.get_new_board(i, i-3, moves))
if not i in [0, 3, 6] : # LEFT 연산자
result.append(self.get_new_board(i, i-1, moves))
return result
✔️ 출력 결과
1
[2, 8, 3]
[1, 6, 4]
[7, 0, 5]
------------------
...
31
[1, 2, 3]
[8, 0, 4]
[7, 6, 5]
------------------
탐색 성공
📍3. 경험적 탐색 방법
☑️ 경험적(휴리스틱) 탐색 방법
문제 영역에 대한 정보나 지식을 사용할 수 있는 탐색 작업
이때 사용되는 정보를 '휴리스틱 정보(heuristic information)'라 함
✔️ 8-puzzle에서의 휴리스틱
- 정확한 정답을 알 수는 없지만, 간접적으로 알 수 있는 지표

📍4. 언덕 등반 기법
✔️ 이 기법에서는 평가 함수의 값이 좋은 노드를 먼저 처리
✔️ 평가함수로 제 위치에 있지 않은 타일의 개수 사용
✔️경험적인 탐색 방법은 무조건 휴리스틱 함수 값이 가장 좋은 노드만을 선택

☑️ 언덕 등반 기법 알고리즘
- 언덕 등반 기법에서는 OPEN과 CLOSED 리스트 사용하지 않음
- 더 높은 곳으로 이동한 후 현 이치보다 더 높은 곳이 없다면 정상에 도달했다고 판단
function HILL_CLIMBING(root)
current ← root
loop do
현재 노드의 자식 노드들을 생성한다.
neighbor ← 평가 함수값이 가장 높은 자식 노드
# 만일 모든 위치가 현 위치보다 낮다면 그 곳을 정상이라고 판단한다
if VALUE(neighbour) ≤ VALUE(current) then
return current
# 현 위치가 정상이 아니라면 확인된 위치 중 가장 높은 곳으로 이동한다.
current ← neighbor
📍5. 최고 우선 탐색
✔️ 지역 최소 문제 (전역에서 봤을 땐 문제가 됨)
- 순수한 언덕 등반 기법은 오직 h(n) 값만을 사용(OPEN 리스트나 CLOSED 리스트도 사용하지 않음)
- 이런 경우에는 생성된 자식 노드의 평가함수 값이 부모 노드보다 더 높거나 같은 경우가 발생할 수 있음
➡️ 지역 최소 문제(local minima problem)
📍6. A* 알고리즘
✔️ 시간 + 방향성을 휴리스틱 정보로 활용하는 알고리즘
✔️ A* 알고지름에서의 평가 함수 값: f(n) = g(n) + h(n)
- h(n): 현재 노드에서목표 노드까지의 거리
- g(n): 시작 노드에서 현재 노드까지의 비용
✔️ A* 알고리즘
AStar_search()
open ← [시작노드]
closed ← [ ]
while open ≠ [ ] do
X ← open 리스트에서 가장 평가 함수의 값이 좋은 노드
if X == goal then return SUCCESS
else
X의 자식 노드를 생성한다.
X를 closed 리스트에 추가한다.
if X의 자식 노드가 open이나 closed에 있지 않으면
자식 노드의 평가 함수 값 f(n) = g(n) + h(n)을 계산한다.
자식 노드들을 open에 추가한다.
return FAIL
☑️ A* 알고리즘 시뮬레이션
✔️ 시작 상태와 목표 상태
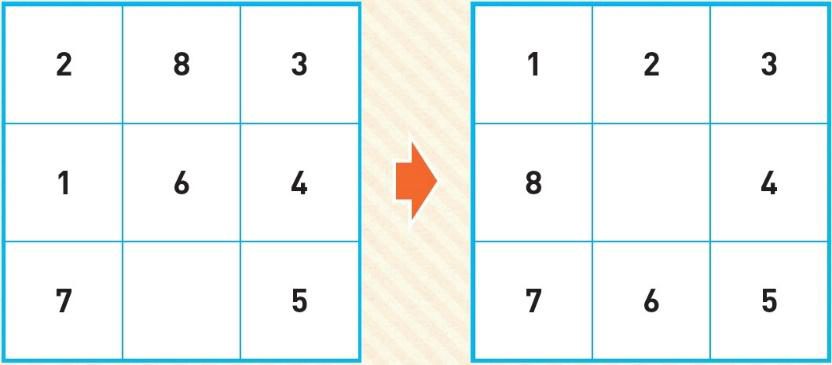
✔️f(n) = g(n) +h(n)
- g(n)은 시작 노드로부터의 거리
- h(n)은 제 위치에 있지 않은 타일의 개수

✔️ A* 알고리즘 구현
import queue
# 상태를 나타내는 클래스, f(n) 값을 저장한다.
class State:
def __init__(self, board, goal, depth=0):
self.board = board # 현재의 보드 상태
self.depth = depth # 깊이
self.goal = goal # 목표 상태
# i1과 i2를 교환하여서 새로운 상태를 반환한다.
def get_new_board(self, i1, i2, depth):
new_board = self.board[:]
new_board[i1], new_board[i2] = new_board[i2], new_board[i1]
return State(new_board, self.goal, depth)
✔️ 클래스 정의
import queue
# 상태를 나타내는 클래스, f(n) 값을 저장한다.
class State:
def __init__(self, board, goal, depth=0):
self.board = board # 현재의 보드 상태
self.depth = depth # 깊이
self.goal = goal # 목표 상태
# i1과 i2를 교환하여서 새로운 상태를 반환한다.
def get_new_board(self, i1, i2, depth):
new_board = self.board[:]
new_board[i1], new_board[i2] = new_board[i2], new_board[i1]
return State(new_board, self.goal, depth)
# 자식 노드를 확장하여서 리스트에 저장하여서 반환한다.
def expand(self, moves):
result = []
i = self.board.index(0) # 숫자 0(빈칸)의 위치를 찾는다.
if not i in [0, 3, 6] : # LEFT 연산자
result.append(self.get_new_board(i, i-1, moves))
if not i in [0, 1, 2] : # UP 연산자
result.append(self.get_new_board(i, i-3, moves))
if not i in [2, 5, 8]: # RIGHT 연산자
result.append(self.get_new_board(i, i+1, moves))
if not i in [6, 7, 8]: # DOWN 연산자
result.append(self.get_new_board(i, i+3, moves))
return result
# f(n)을 계산하여 반환한다.
def f(self):
return self.h()+self.g()
# 휴리스틱 함수 값인 h(n)을 계산하여 반환한다.
# 현재 제 위치에 있지 않은 타일의 개수를 리스트 함축으로 계산한다.
def h(self):
score = 0
for i in range(9):
if self.board[i]!=0 and self.board[i] != self.goal[i]:
score += 1
return score
# 시작 노드로부터의 깊이를 반환한다.
def g(self):
return self.depth
def __eq__(self, other):
return self.board == other.board
def __ne__(self, other):
return self.board != other.board
# 상태와 상태를 비교하기 위하여 less than 연산자를 정의한다.
def __lt__(self, other):
return self.f() < other.f()
def __gt__(self, other):
return self.f() > other.f()
# 객체를 출력할 때 사용한다.
def __str__(self):
return f"f(n)={self.f()} h(n)={self.h()} g(n)={self.g()}\n"+\
str(self.board[:3]) +"\n"+\
str(self.board[3:6]) +"\n"+\
str(self.board[6:]) +"\n"
✔️ 상태 세팅
# 초기 상태
puzzle = [2, 8, 3,
1, 6, 4,
7, 0, 5]
# 목표 상태
goal = [1, 2, 3,
8, 0, 4,
7, 6, 5]
# open 리스트는 우선순위 큐로 생성한다.
open_queue = queue.PriorityQueue()
open_queue.put(State(puzzle, goal))
✔️ 탐색 구현
closed_queue = [ ]
depth = 0
count = 0
while not open_queue.empty():
current = open_queue.get()
count += 1
print(count)
print(current)
if current.board == goal:
print("탐색 성공")
break
depth = current.depth+1
for state in current.expand(depth):
if state not in closed_queue and state not in open_queue.queue :
open_queue.put(state)
closed_queue.append(current)
else:
print ('탐색 실패')
✔️ 실행 결과
1
f(n)=4 h(n)=4 g(n)=0
[2, 8, 3]
[1, 6, 4]
[7, 0, 5]
...
7
f(n)=5 h(n)=0 g(n)=5
[1, 2, 3]
[8, 0, 4]
[7, 6, 5]
탐색 성공
📍6. TSP( travelling salesman problem, 외판원 순회 문제)
✔️TCP에서의 휴리스틱
- 아직 방문하지 않은 도시 중에서 가장 가까운 도시를 다음 방문 도시로 선택하는 것
➡️ 최근접 휴리스틱휴리스틱(Nearest Neighbor Heuristic)
✔️ TSP
- 현재 상태에서 남은 점들을 최적 경로로 돌았을 때 총 거리
( = 아직 방문하지 않은 점들 중 하나를 방문했다고 가정하고, 그 점을 제외한 나머지 점들을 마저 돌았을 때의 거리)
- 효과적으로 짧은 경로를 비교적 신속하게 산출함
✔️ TSP 예시
다음과 같은 6개의 도시와 그들간의 거리가 인접 행렬로 주어졌다고 가정
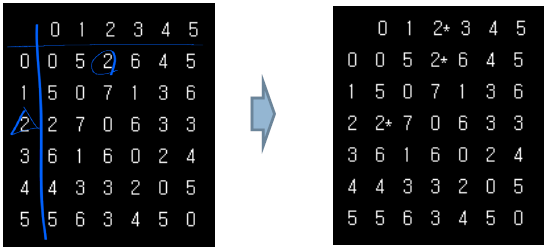
➡️ 0 → 2 → 5 → 4 → 3 → 1 → 0 순서로 도시를 방문
'인공지능' 카테고리의 다른 글
| [인공지능원론] 4. 전문가 시스템 (0) | 2025.04.14 |
|---|---|
| [인공지능원론] 3. 게임트리 (0) | 2025.04.14 |
| [인공지능원론] 2. 탐색(Search) - (1) (0) | 2025.03.20 |
| [인공지능원론] 1. 인공지능 소개 (1) | 2025.03.20 |



